Archimedean Solids in Sacred Geometry
The Archimedean Solids in Sacred Geometry are among the most fascinating shapes in mathematics and metaphysics. These 13 semi-regular polyhedra bridge the pure perfection of the Platonic Solids with the dynamic complexity of the universe. Each solid has a unique balance of symmetry, harmony, and proportion, making them symbols of the hidden order that underlies both nature and spirituality.
From ancient Greece to Renaissance Europe, from cosmic philosophy to modern architecture, Archimedean Solids reveal the universal principle that behind apparent chaos lies geometric order.
Origins of Archimedean Solids
The Archimedean Solids are named after the Greek philosopher Archimedes, who first described them in detail. His original writings are lost, but later mathematicians such as Pappus of Alexandria preserved his insights. During the Renaissance, figures like Johannes Kepler rediscovered and cataloged these shapes, giving them Latin names and linking them to cosmic harmony.
Plato had earlier described the five Platonic Solids, which represent the classical elements of fire, earth, air, water, and ether. The Archimedean Solids expand this sacred geometry system, combining multiple polygons while still maintaining perfect symmetry. They serve as a bridge between the pure elemental forms of Plato and the more complex designs seen in nature and architecture.
Sacred Symbolism of the Archimedean Solids
In Sacred Geometry, these 13 forms are more than mathematical curiosities. They symbolize the interplay between unity and diversity—the way multiple shapes combine into a greater harmony. Each vertex of an Archimedean Solid touches the surface of a sphere, suggesting cosmic wholeness and the interconnectedness of all things.
Some traditions see the Archimedean Solids as energetic templates, part of the same universal blueprint that includes the Flower of Life and Metatron’s Cube. Just as the Platonic Solids are considered the “building blocks of the cosmos,” the Archimedean Solids represent the refinement of that design into living patterns of transformation and evolution.
Examples of Archimedean Solids
- Cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.
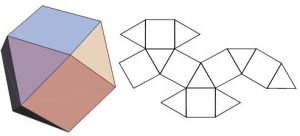
- Great Rhombicosidodecahedron
In geometry, a truncated icosidodecahedron – rhombitruncated icosidodecahedron – great rhombicosidodecahedron – omnitruncated dodecahedron or omnitruncated icosahedron – is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces. It has 62 faces: 30 squares, 20 regular hexagons, and 12 regular decagons. It has the most edges and vertices of all Platonic and Archimedean solids, though the snub dodecahedron has more faces.
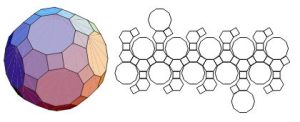
- Great Rhombicuboctahedron
In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry (equivalently, 180° rotational symmetry), the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism. Alternate interchangeable names are: Truncated cuboctahedron (Johannes Kepler), Rhombitruncated cuboctahedron (Magnus Wenninger), Great rhombicuboctahedron (Robert Williams), Great rhombcuboctahedron (Peter Cromwell), Omnitruncated cube or cantitruncated cube (Norman Johnson), Beveled cube (Conway polyhedron notation).
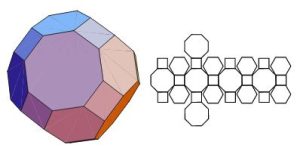
- Icosidodecahedron
In geometry, an icosidodecahedron is a 32-faced polyhedron. An icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.
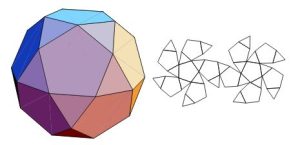
- Rhombicosidodecahedron
In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal non-prismatic solids constructed of two or more types of regular polygon faces. It has 20 regular triangular faces, 30 square faces, 12 regular pentagonal faces, 60 vertices, and 120 edges.
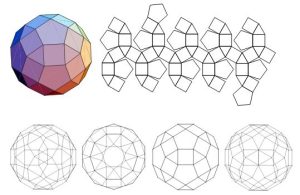
- Small Rhombicuboctahedron
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square (equivalently, all the edges are the same length, ensuring the triangles are equilateral), it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.
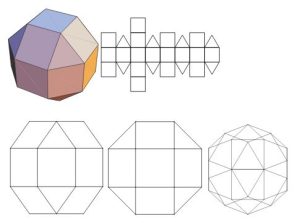
- Snub Cube
In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid with 38 faces: 6 squares and 32 equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron; that is, it has two distinct forms, which are mirror images (or “enantiomorphs“) of each other. The union of both forms is a compound of two snub cubes, and the convex hull of both sets of vertices is a truncated cuboctahedron.
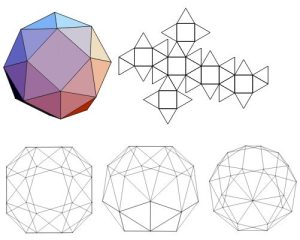
- Snub Dodecahedron
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal non-prismatic solids constructed by two or more types of regular polygon faces. The snub dodecahedron has 92 faces (the most of the 13 Archimedean solids): 12 are pentagons and the other 80 are equilateral triangles. It also has 150 edges, and 60 vertices.
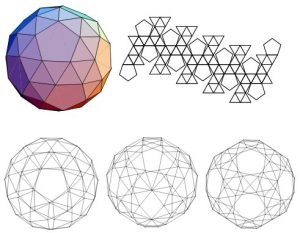
- Truncated Cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces (6 octagonal and 8 triangular), 36 edges, and 24 vertices. The truncated cube has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: triangles, and octagons.
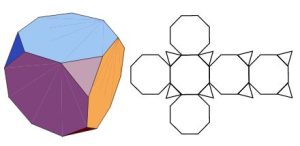
- Truncated Dodecahedron
In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges. This polyhedron can be formed from a regular dodecahedron by truncating (cutting off) the corners so the pentagon faces become decagons and the corners become triangles. It is used in the cell-transitive hyperbolic space-filling tessellation, the bi-truncated icosahedral honeycomb.
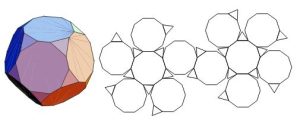
- Truncated Icosahedron
In geometry, the truncated icosahedron is an Archimedean solid, one of 13 convex isogonal non-prismatic solids whose 32 faces are two or more types of regular polygons. It is the only one of these shapes that does not contain triangles or squares. In general usage, the degree of truncation is assumed to be uniform unless specified. It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges. This geometry is associated with footballs (soccer balls) typically patterned with white hexagons and black pentagons. Geodesic domes such as those whose architecture Buckminster Fuller pioneered are often based on this structure. It also corresponds to the geometry of the fullerene C60 (“buckyball“) molecule.
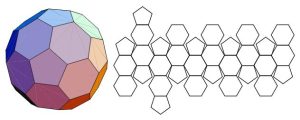
- Truncated Octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron’s vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 edges, and 24 vertices. Since each of its faces has point symmetry, the truncated octahedron is a 6-zonohedron. Like the cube, it can tessellate (or “pack”) 3-dimensional space, as a permutohedron. The truncated octahedron was called the “mecon” by Buckminster Fuller.
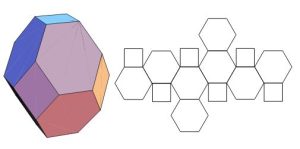
- Truncated Tetrahedron
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncating all 4 vertices of a regular tetrahedron at one third of the original edge length. A deeper truncation, removing a tetrahedron of half the original edge length from each vertex, is called rectification. The rectification of a tetrahedron produces an octahedron.
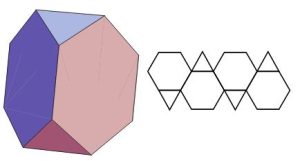
Practical Applications of Archimedean Geometry
These shapes are not only symbolic but also practical. They appear in:
-
Nature: Crystals, viruses, and molecular patterns often mirror Archimedean symmetry.
-
Architecture: From Islamic mosaics to modern geodesic domes, Archimedean Solids guide design.
-
Meditation & Energy Work: Visualizing these solids can help practitioners align with universal harmony and expand consciousness.
By studying Archimedean Solids in Sacred Geometry, we gain insight into both the visible patterns of creation and the unseen spiritual order.
Conclusion: A Cosmic Blueprint
The Archimedean Solids remind us that geometry is not only mathematics but also metaphysics. They unite science, art, and spirituality into a single vision of the cosmos. Just as the ancients saw the Platonic Solids as the foundation of reality, the Archimedean Solids suggest that the universe evolves through symmetry, balance, and sacred design.
They are living symbols of the eternal truth: the universe is built on geometry, and geometry is sacred.
–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
References
- Sacred Geometry Number symbolism – Pythagoreanism, Numerology, Mysticism | Britannica
- Sacred Geometry Secrets Universe Sacred Geometry: Unlocking the Secret Structures of the Universe | Ancient Origins
- Weisstein, Eric W. “Archimedean Solid.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/ArchimedeanSolid.html
- Sacred Geometry Sacred Geometry Archives – Ancient360